2進数とは何か、10進数から読み解く。

はじめに

この記事では、2進数の考え方を説明していきます。
2進数とは0と1を使って数を表す方法またはその方法であらわされた数のことを指します。0と1の羅列だということ以外正直よくわかっていないという人は多いと思います。この記事はそんな人のためのものです。記事を読み終わるころには、「2進数」「重み」「基数」を理解できます！

この記事の要点は

ということです。難しく考える必要はありません。10進数でも2進数でも本質は同じなのです！

「10」は「1」と「0」でできている

簡単に10進数をおさらいしましょう。

10進数は10個の数字を使って数を表す

私たちは、ものを数えるとき、何もない場合は0ということができます。そして数が増えるごとに1,2,3,4,5,6,7,8,9と続きます。合計10個の数字で10進数はあらわされるのです。

ここで質問です。「10」は一つの数字でしょうか。それとも「1」と「0」でできているのでしょうか。

10進数のルール

「10」は、見た目で桁ごとに分解すると「1」と「0」になります。桁の意味するところは10が1個、1=10⁰が0個あるということです。

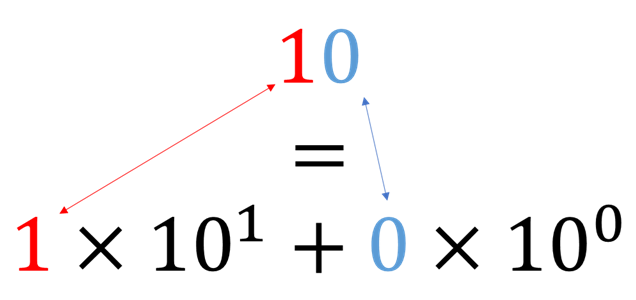
10進数は、位に応じて10の累乗がいくつあるかというのを表しているのです。十の位や百の位などを小学生のとき習ったことを思い出してきたでしょうか。この「10の累乗」の部分を桁の重みといいます。

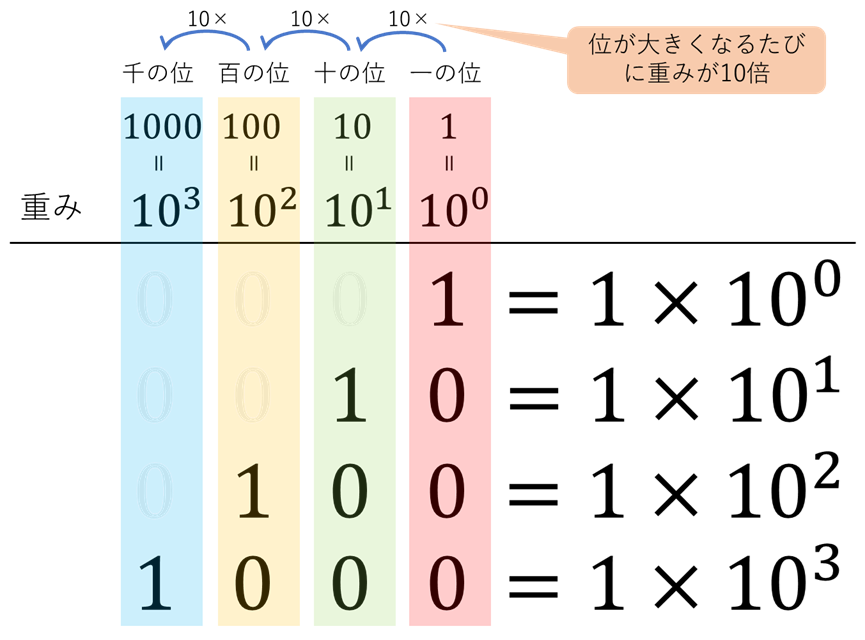
さて、なぜ10進数の桁の重みは10の累乗なのでしょう。
それは10進数が0～9の数字しか使わないゆえに10ごとに桁上がりするからです。ある位の重みが10個集まると一つ上の位の「1」になります(例：百の位の重みは「$100=10^2$」、十の位の重みは「$10=10^1$」)。だから位が上がるごとに10倍ずつ増えていくのです。
どの桁にも共通して存在する基本的な数、それが基数です。10進数の基数は「10」です。

ためしに「365」という数を分解してみましょう。365は読むと「三百六十五」です。読んで字のごとく、3つの百ひゃくと6つの十じゅうと5つの一いちです。百、十、一が桁の重みに当たります。
数式で表すと$365=3\times100+6\times10+5\times1=3\times10^2+6\times10^1+5\times10^0$です。

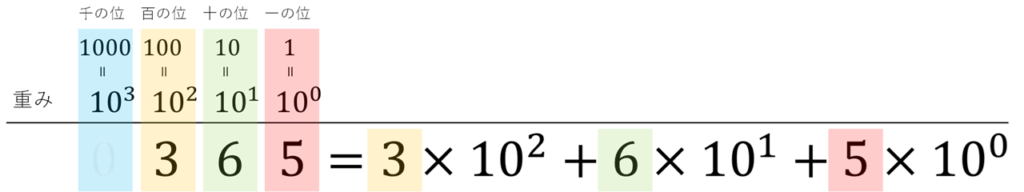
2進数も考え方は同じ！

10進数のおさらいが済んだら2進数を見ていきましょう。考え方はどちらも同じです。違うのは、使う数字の数だけ。

2進数は、0~1の2個の数字を使って数を表現します。

2進数も10進数と同じように0,1とカウントし、2進数には1までの数字しかありませんからより大きな数を表すためには桁上がりをします。9より大きい数を表すときに桁上がりする10進数と同じです。

数の後ろの(2)や(10)はn進数の数であることを表しています。

2進数	10進数
$0_{(2)}$	$0_{(10)}$
$1_{(2)}$	$1_{(10)}$
$10_{(2)}$	$2_{(10)}$
$11_{(2)}$	$3_{(10)}$
$100_{(2)}$	$4_{(10)}$
︙	︙

2進数では、1を2個集めたら桁上がりして$10_{(2)}$、10進数でいう「2$=2^1$」になるわけです。さらに$10_{(2)}$を2個集めると桁上がりして$100_{(2)}$、10進数でいう「4$=2^2$」になります。さらに、$100_{(2)}$を2個集めると桁上がりして$1000_{(2)}$、10進数でいう「8$=2^3$」になります。
あとは同じことです。2進数の桁の重みは倍倍になっていきます。以上の関係から2進数の重みは$2^x$と表せることがわかると思います。2進数の各桁は$2^x$が何個あるかというのを表しているわけです。「2」が2進数の基数です。

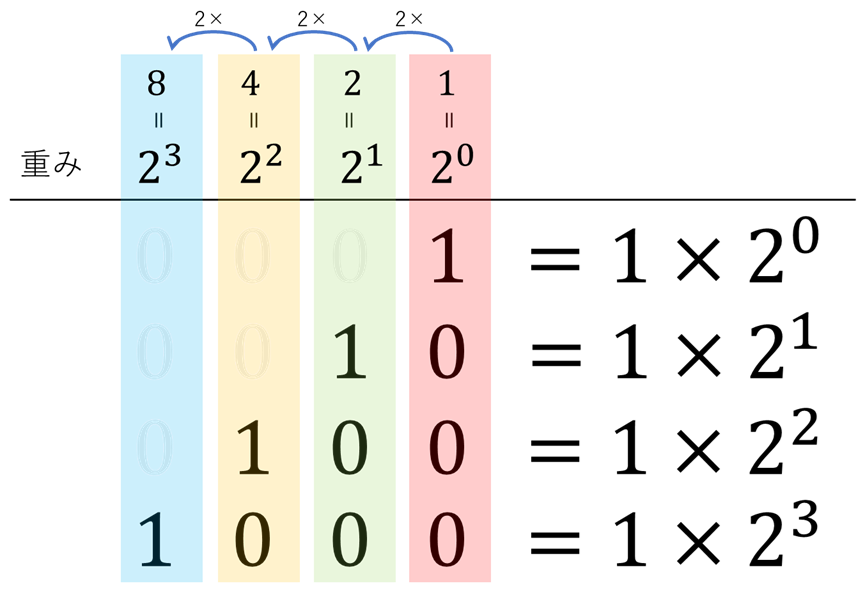
2進数の仕組みが分かったところで「$11011_{(2)}$」という数を分解してみましょう。

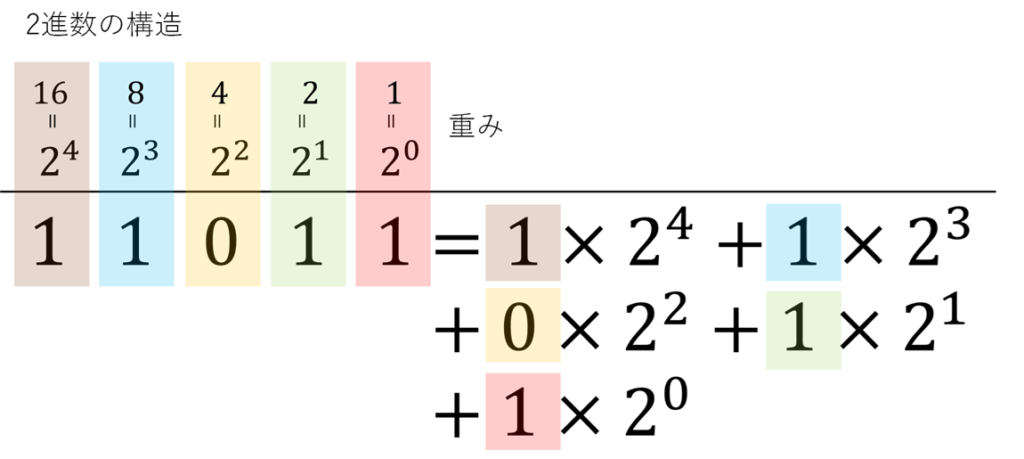
$11011_{(2)}=1\times2^4+1\times2^3+0\times2^2+1\times2^1+1\times2^0=16+8+0+2+1=27$と10進数に変換することができました。

練習

問題を解くことによって、理解を深めましょう！

$110110_{(2)}$を10進数で表せ。

答え(クリックで展開できます)

$110110_{(2)}=1\times2^5+1\times2^4+0\times2^3+1\times2^2+1\times2^1+0\times2^0=32+16+0+4+2+0=54$

まとめ

ここまでお疲れさまでした。さて、まとめに入りましょう。

重要なのは「10進数も2進数も各桁の重みがいくつあるかを表している」ということです。桁の重みが10進数と2進数で違うのは使われる数字の数が違うことによるものでしたね。2進数と10進数の違いをまとめてみました。

	2進数	10進数
何個の数字が使われるか	2個(0～1)	10個(0～9)
基数	2	10
重み	20, 21, 22 など	100, 101, 102 など

この記事が理解の一助になれば幸いです。ありがとうございました。